"A Just
Cause"
©
Paul Serotsky 1998, 2004
Continued .... Part
2
Part
1 Part
3
Tonality
A musical scale does
not of itself a "tonality"
make. Tonality is something which
makes a certain subset of identities
"belong" together, which implies some
underlying rule over and above that
which defines the degrees of the scale.
In ET, a "key" is obtained by dividing
up the intervals of the "octave":
|
Scale
|
D
|
D#
|
E
|
F
|
F#
|
G
|
G#
|
A
|
A#
|
B
|
C
|
C#
|
D
|
|
Selection
|
D
|
|
E
|
|
F#
|
G
|
|
A
|
|
B
|
|
C#
|
D
|
|
Intervals
|
|
1
|
|
1
|
˝
|
1
|
|
1
|
|
1
|
˝
|
You can see the
well-known pattern of tones and semitones:
two groups of tone-tone-semitone,
separated by a single tone. This whole
template can simply be shifted up
the scale, a semitone at a time, to
generate all the 12 major keys. This
exact translational symmetry is because
all the intervals are exactly the
same size. But, is there any intrinsic
reason WHY? Is this pattern God-given,
or what? Is there any good reason
why not a sequence [1, ˝, 1, ˝, 1,
˝, 1, ˝], or anything else? And, note,
we haven't yet given any thought to
the "minor" keys, which in ET are
a veritable can of worms.
Let's consider tonality
in a JI system. A ratio involves two
numbers. Each individual number represents
a potential identity, because
once any permitted second number is
given, an identity becomes defined.
If one number (say the lower) is fixed,
it becomes a numery nexus (i.e.
"anchor point"). Ratios with a given
numery nexus are related by that nexus
- they have something in common. The
ratios 1/1, 5/4, 3/2 (where 1, 2,
and 4 are equivalent - merely different
"octaves", and hence not different
identities) from the 5-limit sequence
are the identities with an under-numery
nexus of 1. The identities 4/3, 5/3,
1/1 (i.e. 3/3) are those with an under-numery
nexus of 3. Similar groups can be
formed having an over-numery
nexus. All these are nothing more
exotic than triads - basic
chords.
But chords are
the stuff of which keys are made.
You can see that this is borne out
by D-F#-A from Table 1. In each of
the examples given above, the numbers
associated with a given numery nexus
are always in the sequence 1, 5, 3
(again allowing for "octave" transpositions),
which is itself a fixed pattern.
Now, this is starting to get interesting,
so take a deep breath and brace yourselves!
If the numery nexus is the lower number
of the ratio, the set of ratios in
the triad are the 1, 5, 3 identities
of an over-number tonality ("otonality"),
in ascending pitch order. Similarly,
if the numery nexus is the upper number,
the ratios are the 1, 5, 3 identities
of an under-number tonality ("utonality"),
in descending pitch order.
That in itself is
an impressive mathematical and aesthetic
symmetry, but there's yet more. While
the members of each triad are in the
same fixed relationship to
one another - the middle identity
is always a 5/4, and the top identity
a 3/2, from the unity of the particular
chord - any particular triad cannot
be transformed into another of the
set by the application of a common
interval. Thus, while they have
identical internal structures,
they are truly distinct from one
another: they are the chords of
different keys.
 It is this distinctness that obviates
the possibility of "transposition"
in JI, one reason often cited for
its "inferiority" to ET which readily
transposes. But the real reason
(again) is operational convenience,
the price being that ET keys are
not truly distinct. JI chords
of different keys may be distinct,
but they are, surprising as it might
seem, nevertheless related. Partch
demonstrated this with a striking
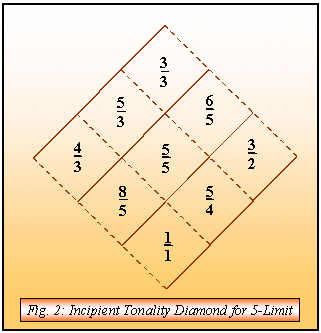
diagram - what he called the Incipient
Tonality Diamond (fig. 2), the
implications of which are truly startling.
All the true triads of the 5-limit
are shown. Triads formed from compound
intervals do not generate tonality,
and so are excluded.
It is this distinctness that obviates
the possibility of "transposition"
in JI, one reason often cited for
its "inferiority" to ET which readily
transposes. But the real reason
(again) is operational convenience,
the price being that ET keys are
not truly distinct. JI chords
of different keys may be distinct,
but they are, surprising as it might
seem, nevertheless related. Partch
demonstrated this with a striking
diagram - what he called the Incipient
Tonality Diamond (fig. 2), the
implications of which are truly startling.
All the true triads of the 5-limit
are shown. Triads formed from compound
intervals do not generate tonality,
and so are excluded.
The sequences ascending
from lower left to upper right between
solid lines are the otonalities, and
those descending from upper left to
lower right between dotted lines are
the utonalities. Once we have tuned
all the intervals of the 5-limit to
a unity (1/1), we have not just one
true triad based on that unity, but
also five other true triads. 1 (or,
equivalently, 2, 4, or 8) is always
part of a ratio which is a unity
("tonic") of a triad, 5 is always
part of a ratio which is the middle
identity ("mediant") of a triad, and
3 (or, equivalently, 6) is always
part of a ratio which is the top identity
("dominant") of a triad - and thus
we have the origin of the terms "mediant"
and "dominant".
From this point,
things start (!) to get a bit difficult
to explain simply, but it should be
fairly clear by now that the 1, 5,
3 "odentities" of an otonality are
a triad of tones in order of ascending
pitch, equivalent to an ET "major"
tonality triad such as C-E-G (or D-F#-A).
The breathtaking corollary is that
the 1, 5, 3 "udentities" of a utonality
are a triad of tones in order of descending
pitch, which is a mirror image
of an otonality. This is the origin
of the ET "minor" tonality triad.
So we find that in JI there is no
mystery about minor tonality: the
major and minor keys coexist of
necessity - like love and marriage,
"you can't have one without the other"!
Any comparison between ET and modern
morality is entirely at the indiscretion
of the reader.
Minor tonality
in ET is difficult to explain, hence
the "mystery" surrounding it. Explanations
are rarely ventured, and I have yet
to find one that is even remotely
convincing. Even Paul Hindemith, for
example, could manage nothing better
than, "the minor is the 'clouding'
of the major", which is, to put it
mildly, somewhat woolly. In the mathematics
and science of JI, as reviewed above,
we find a far clearer and utterly
convincing explanation of the origins
of tonality, one that presents tonality
as a part of the natural order. Borrowing
Hindemith's phrase, we might be led
to conclude that ET "is the 'clouding'
of" JI. ET now really begins to look
more like an artificial simulation
of the fabric of tonality (shades
of The Song of the Nightingale?),
something that really was manufactured
to suit the convenience of keyboard
design and musical annotation.
However, it was also
promoted with a religious zeal, quite
literally so in some cases, notably
by those who were in pursuit of the
"Holy Grail" of a "circle of fifths",
to the altar of which JI had to be
sacrificed to propitiate the false
gods of "Perfection". In JI, if you
ascend the scale a fifth at a time,
you will never drop onto an
identity which is an exact number
of octaves above your starting point.
In ET's logarithmic world, which looks
the same wherever you view it from,
you can not only have a circle of
fifths, you can also have a circle
of thirds, fourths, or whatever you
fancy.
This whole business
arose from a general superstitious
concern over the "perfection" of the
circle, it being argued that there
must be a "circle" in something as
holy and mystical as music. Big Deal.
With his extreme disillusionment with
the apparently corrupt state of Music,
it is easy to see what it was about
JI that so excited and inspired Harry
Partch.

But, what happens
if we apply the Incipient Tonality
Diamond concept to ET? The short answer
is: we get a reasonable, and
long overdue, explanation of the origin
of ET Minor Tonalities. Fig. 3
illustrates the pattern, with the
equivalents to the original JI 5-Limit
tonality generating identities shown
in BOLD. The full set of 12
identities is shown. In ET, all contribute
equally to tonality generation, as
all are smoothed into equality by
the logarithmic formula. Bearing in
mind that ET is a formulaic mathematical
approximation of JI, let's see what
happens if we follow the same procedure.
First, we lay out
the C Major scale (shaded), ascending
from the bottom towards the right.
The "tone-tone-semitone" groupings
are mapped and bracketed for clarity.
On the lower left, the 12 identities
are laid out in order of descending
pitch, from the bottom to the
left. The Major tonalities can readily
be seen starting on the lower left
edge, each running between a pair
of solid lines towards the upper right,
and having exactly the same pattern
offset by a semitone at a time. So
far, so good.
Minor tonalities
should be revealed, in descending
pitch order, by reading off the scales
starting at the bottom right edge
and going towards the top left (between
the dotted lines, as before), following
the descending tone-tone-semitone
groupings. Try it. It doesn't quite
work, does it? The sequence you find,
compared with the ET scales of C minor,
is

The identities which
do not correspond in the ET scales
are shown shaded. The lack of exact
correspondence, and the reason there
are three variants, is because
the ET minor scale has been "doctored"
(a minor sin to someone who has just
vandalised the entire world of tonality!).
The Descending Melodic Minor is closest,
and interestingly if you read off
the sequence starting on the C in
the G major row, equivalent to the
top corner of the "real" ET Incipient
Tonality Diamond, you will find an
exact correspondence - though why
I'm not sure! The A# is replaced by
a B in the Ascending Melodic Minor
to re-establish a semitonal leading
note, with the G# lifted to A to avoid
the "discomfort" of the augmented
second opened up in the process. There
are a couple of other "fudges", presumably
for similar reasons but nevertheless
there it is, in all essential aspects:
the origin of the Minor.
4 Monophony
A JI system is built on a single,
generating "prime unity" (1/1 ratio). Any such system
is termed a monophony. The prime unity is
the root of the entire scale. You could say that
JI is like a universe with a centre. In ET, the
choice of a reference pitch (A=440 Hz, for example)
is purely a matter of convenience for tuning. If
we chose a frequency for A corresponding to a displacement
of a whole number of semitones, for instance 493.883
Hz (the frequency corresponding to B), the ET scale
would be identical: only the names of the identities
would be different.
The only observable effect would
be that instruments would have to transpose a tone.
Even with a pitch shift which is not a whole number
of semitones, the impact on ET is no more than the
adjustment of an instrument's basic "length".
However, if the JI prime unity is changed in any
way at all, a completely different scale
would be created, and all your instruments would
have to be retuned - or even reconstructed. In JI,
it seems, you cannot easily tinker with "concert
pitch"!
Partch's first job was to construct
his monophony. He had two tasks, the first of which
was comparatively, but not completely, trivial:
to decide his prime unity. He chose the pitch of
the G below middle C of ET, a decision, I suspect,
not unrelated to the fact that many of his early
experiments were carried out using a viola!
The second task was nothing like
as simple: to specify the identities of his monophony.
Of course, he could simply have reversed the process
which created the ET scale (as per the table), but
this brought him up against one of his objections
to the musical establishment. He was only too well
aware that the introduction of ET had stopped further
evolution of tonality dead in its tracks: this was,
after all, one of the aspects of ET that he found
so unacceptable.
Up to that time, there had been
a slow but inexorable evolution of tonality, as
JI intervals of greater relative dissonance (ratios
using higher numbers) were called on to expand,
by inserting further intervals and without modifying
existing ones, the range and resolution of the intonational
system. This kind of development is much more difficult
in ET - evidently so, because the scale has changed
not one jot in the 300-odd years of its existence.
The musical scale was frozen solid on the equivalent
of the 5-limit. This implies a limitation of expressive
potential of just the same sort which the JI system
simply stepped over by extending into the 5-limit
in preference to the 3-limit.
The so-called "breakdown of
tonality" precipitated by late Nineteenth Century
chromaticism and culminating in Twentieth Century
serialism was the direct consequence. It can be
recognised that composers were actually battering
on the prison walls of the implicit 5-limit of ET.
We can thus see that Wagner, Strauss, Schoenberg
et al were not trying to do away with tonality,
rather they were desperate to expand it.
In the event, unable to escape from the sonic strait-jacket
of ET, the only recourse was to move even further
from the natural landscape of JI, and one is forced
to ask, "Is this is why most people find dodecaphonic
music so hard to swallow?"
In this context, Partch saw that
the implicit freezing of the 5-limit in ET suggested
a history of under-use of the ear's abilities. Using
physiological data, and experiments of his own,
he discovered that the average human ear was capable
of resolving and recognising far narrower intervals
and differences of pitch than ET would permit.
Partch concluded that there was
every reason why his monophony ought to be based
on the abilities of the very organ which it was
designed to serve - the human ear. After further
research and experimentation, he found that the
appropriate limit was not merely the 7, but the
11! This resulted in a scale comprising some 28
true identities, which were augmented by 15 multiple
number ratios, giving 43 tones to the "octave" (almost
entirely gratifying aficionados of The Hitch-hiker’s
Guide to the Galaxy!).
These are Partch's chosen identities:
|
1/1
|
81/80
|
33/32
|
21/20
|
16/15
|
12/11
|
11/10
|
10/9
|
9/8
|
8/7
|
7/6
|
|
32/27
|
6/5
|
11/9
|
5/4
|
14/11
|
9/7
|
21/16
|
4/3
|
27/20
|
11/8
|
7/5
|
|
10/7
|
16/11
|
40/27
|
3/2
|
32/21
|
14/9
|
11/7
|
8/5
|
18/11
|
5/3
|
27/16
|
|
12/7
|
7/4
|
16/9
|
9/5
|
20/11
|
11/6
|
15/8
|
40/21
|
64/33
|
160/81
|
(2/1)
|
The true identities
(the pure 11-limit ratios) are shown
in bold. Some of the multiple
number ratios in my earlier table
do not feature here, partly because
my derivation is somewhat conjectural,
but largely because Partch was carefully
selective from the huge range of choices.
In some cases there were simpler ratios
of 7 or 11, for example he preferred
14/11 (= 1.273) to 32/25 (= 1.280).
However, he meticulously ensured that
his monophony embraced intact all
the ancient modes, including Greek
and Church. Practically all of the
scales prevalent in the rest of the
world's "classical" and "folk" music
- which can only be approximated on
the piano, as Bartok was well aware
- are also present and correct.
Partch's choice of
a 43-tone scale was thus not, as is
commonly supposed, a product of the
arbitrary ravings of a crank and a
crackpot, but the logical and reasonable
conclusion of much careful scientific
study. Music using this scale to its
full potential may sound strange and
hard to accept, but it is no more
so than any other music which transgressed
the bounds of what was harmonically
"acceptable" at the time.
5 Notation
Looking first at
the notational style of ET, and then
at the table of 43 identities, Partch
found himself confronted with a major
headache. His first option, if he
were to write music for players to
play, was to adapt the existing notation
in respect of pitch representation.
If each identity were to have a line/space
to itself, this would imply a stave
of around 27 lines, bearing in mind
that JI does not enjoy the symmetry
of ET which invites the convenience
of #, =,
and >.
To have a stave with few enough lines
to be practical, a substantial and
complex symbology for the identities
would be required. But, where would
you put the symbol? The obvious space
is taken up by notation of duration.
Partch's solution
(to cut a long story short) was supremely
pragmatic: forget the stave to represent
pitch, he would use the ratios
themselves, with duration noted
as a "suffix".
It quickly became
apparent that his general notation,
although fine for composing, was too
complicated and clumsy for performance
use. This he resolved by developing,
for each instrument, a specialised
notation which was less complicated
and thus easier to read.
Part
3 Part
1
|
Error processing SSI file
|

