"A Just
Cause"
©
Paul Serotsky 1998, 2004
1 Introduction
"What rubbish!"
Two little words of deprecation, hardly
an auspicious start to a train of
events which was to transform my attitude
to music. I heard them from a lady
sitting just behind me at a presentation
given, in 1976, by a representative
of a record distributor. We had just
heard an extract from one of the CRI
(Composers' Recordings Incorporated)
records his company was then marketing
in this country. To be fair, the lady
was merely giving voice to an opinion
held by many, if not most, of the
audience. However, I have to admit
that I find it intensely aggravating
when an extended musical work is summarily
dismissed on the strength of a short
extract, and anyway the bit of music
that we had heard didn't sound all
that bad to me. Nevertheless,
it was quite unlike anything I had
hitherto experienced, which I suppose
makes it fairly "way out", and spurred
by the general scorn, my inherent
bloody-mindedness dictated that I
investigate further.
As luck would have
it, a combination of relative impecunity
- a perennial problem for a "working
class" record collector - and abject
failure of local record shops to connect
with the source of supply prevented
me from getting hold of a copy of
the record. So, end of story? Well,
almost but, as you might guess, not
quite. Fully four years went by, before
two unrelated events rekindled my
curiosity. The first was an item in
the Bulletin of the (then)
National Federation of Gramophone
Societies, wherein the editor, the
late Bill Bryant, to whom I shall
be eternally grateful, let it slip
that he had actually got hold of several
of those CRI records, including that
particular one.
A year further down
the line, researching for a projected
Huddersfield Gramophone Society programme
on "Music from the New World", I came
across a reference to a book called
Genesis of a Music. The authorís
name was the same as the composer
of that scorned musical extract. Coincidence?
Not likely: letís face it, Harry
Partch is not the sort of name
that overburdens the telephone directory.
I checked the index in the Bradford
Library, and to my utter amazement
found that the book was actually on
the shelf! Borrowing it, I found it
a substantial tome of well over 500
fairly large pages, which I read from
cover to cover - twice! What
I found there, though understood only
in part and then with some difficulty,
convinced me that I should make Harry
Partch the centrepiece of my programme,
with the help of the loan of one of
Bill's records.
By now you have every
right to ask, especially if on one
particular occasion you had dismissed
a fragment of very strange-sounding
music with a summary "What rubbish",
just what it was that "transformed
my attitude to music"? Let me try
my best to explain . . .
2 Partch's
Achievement
That lady was in
good company: no less a personage
than Norman Lebrecht has also dismissed
Partch, calling him a "crackpot inventor".
On this occasion at least, good old
Norman is talking right out of the
back of his head. I discovered that
the California-born Harry Partch,
far from being simply a "crackpot
inventor" and composer of "rubbish",
is in fact an archetypal "pioneer",
riding his covered wagon westward
into musical territories to all modern
intents and purposes utterly uncharted.
He turns out to be one of the most
original musicians of this century,
if not in the entire history of the
music of Western Civilisation.
As a young man, Partch
(1901-74) became increasingly dissatisfied
with the entire "business" of music,
with its widespread emphasis, both
by teachers and authors, on high levels
of instrumental skills and on playing
and composing "technique". That is,
if a work was "polished" in performance
or compositional technique then it
was automatically "good", if a player
was extremely dexterous then he was
ipso facto an "artist", and
if he could play in such a way as
to please the "experts" - whoever
they might be - then he was, equally
ipso facto, a "great artist" [Genesis
of a Music, p4].
What seemed to irk
Partch so much was that everyone was
busily fêting the virtuosi and
indulging in strictly ritualised concerts,
but no-one seemed to be giving any
real thought to the intrinsic value
of the materials with which they were
working - and here he meant not just
the basic philosophical attitudes,
but the very organisation of
sounds which distinguishes "music"
from "noise".
He wasn't over the
moon about music schools and teachers,
either. Music, of all the Arts, seems
to be the only one whose proponents
steadfastly refuse to "demean" themselves
by acquaintance with the science in
their art. Thinking about it, such
is the mystique surrounding Music
as an art that one of the surest ways
of precipitating a fit of apoplexy
in a musician is to suggest that Music
is a branch of mathematics.
Worse, Partch found that the little
"science" that was taught was at best
superficial, often sketchy, and at
worst completely spurious.
Apparently, what
he found so utterly exasperating was
that Music was presented as something
immutable, even sacrosanct: the
student was fed rules and regulations
by rote, and if he dutifully learned
and practised them he would become
a "good musician". But, it seemed
to be forbidden to question the validity
of the quasi-biblical "rules", or
to enquire into the whys and wherefores
of the structure of the art. The reason?
TRADITION, or, more bluntly, "fossilisation".
We had better and better pianists,
conductors, composers, we increased
the range of our "good" music, but
the tradition itself remained undisturbed
because the ideas and objects at the
heart of the art were not challenged
and investigated, not even by the
supposed "avant-garde".
So, even in his teens,
he had more or less given up on the
musical system and establishment of
modern Europe. He turned to the public
libraries in a search for material
from which to learn. At the ripe old
age of 21 he came across the key to
his dilemma, a work not of musicology
but of physics: Ellis' translation
of On the Sensations of Tone,
by Helmholtz. This so convinced him
that the traditional system was rotten
in its very foundation - in its implementation
of the concept of "tonality" - that
he made an almost unimaginably bold
decision, one that would freeze the
blood in the veins of most mortals.
Consigning his entire musical output
to date to the tender mercies of a
pot-bellied stove was a gesture both
practical and symbolic: he turned
his back on the current musical tradition
and, working from first principles,
set out to create an entire Music
of his own from scratch.
3 The Tonal
System
The first thing Partch
needed to determine was the tonal
system in which his music would operate.
To be true to his principles, he could
not just throw out the "traditional"
one and concoct another one willy-nilly.
To succeed, he had to be committed
to justifying, scientifically and
practically, whatever he devised.
This is such a fundamental step that
it bears reviewing in some detail.
Fortunately, it is also a fascinating
and revealing - though (be warned!)
difficult - subject. It might help
to be aware that what follows is ultimately
derivable, believe it or not, from
the simple physics of a vibrating
string such as we are all taught at
school. True, this same basis is often
used in conventional music theory,
but as we shall see its application
is fundamentally flawed.
Ring Out the New
. . .
As we all know, the
scale now used universally in all
music of the Western European tradition
- be it "classical", "popular", "jazz",
or whatever - is that playable on
a piano keyboard. The "octave" is
divided into 12 equal intervals, or
"semitones", appropriate selections
of eight of which provide all the
"keys": 12 "major" and 12 "minor".
And are we not taught in school of
the birth of this intonational system
as if it were the Messiah of some
religion (with J S Bach in the role
of John the Baptist)? If not, we may
as well be, for all that we learn
of what it really is and how
it really works.
Most "traditional"
musicians would probably recoil in
horror if told that each degree (note)
of the scale is determined exactly
by multiplying the frequency of the
previous degree by a factor of 21/12
- that the Holy Musical Scale should
be derivable by mere common mathematics!
But worse, much worse, is to come.
The ONLY truly consonant interval
of this hallowed system, 12-tone
equal temperament (ET), is the
octave, that is the interval
between two degrees such as C and
C'. ALL, bar none, of the so-called
major intervals and chords (such as
C-E-G-C), are dissonant! ALL, bar
none, of the other chords and intervals
are more dissonant!
We will come to the
meanings of "consonant" and "dissonant"
in a moment. I recall a TV documentary
in which no less a figure than Olivier
Messiaen explained his characteristic
chord structures. He played a sequence
of notes on a piano and proclaimed,
"There! I have played all the harmonics."
With due respect, he was wrong on
not one but two counts. Firstly and
perhaps a little pedantically, he
had played only a dozen or so notes,
which is rather too few to constitute
"all the harmonics". Secondly and
rather more crucially, he had played
none of the harmonics, other
than the octaves of his chosen fundamental.
Galileo penned a
perceptive and penetrating observation:
"Agreeable consonances
are pairs of tones which strike
the ear with a certain regularity;
this regularity consists in the
fact that the pulses delivered by
the two tones, in the same interval
of time, shall be commensurable
in number, so as not to keep the
eardrum in perpetual torment, bending
in two different directions in order
to yield to the ever-discordant
impulses."
This holds the key
to "consonance" and "dissonance".
What it means is that, at regularly
occurring instants, the two vibrations
will be in step, and, as any mathematician
or physicist will tell you, this is
possible only if the frequencies
of the two tones are in whole-number
proportions. Moreover it follows,
partly from Galileo's statement, that
the degree of consonance of an interval
decreases from 1/1 (unison, where
the frequencies are equal) as the
size of the whole numbers involved
increases. This is because the tones
are in step less often. With big enough
numbers the interval eventually approaches
"complete" dissonance, as the tones
are in step so rarely that the ear
can no longer perceive the regularity
of the pattern.
The limit of this
progression from absolute consonance
to absolute dissonance comes when
the numbers become infinitely large,
in that remote realm where the rational
number locks horns with its irrational
counterpart. The "irrational number"
is a thoroughly nasty beast: it cannot
be exactly represented by the ratio
of two whole numbers or, equivalently,
requires an infinite sequence of non-recurring
decimal digits (B
is the classic example).
Since the adjacent
degrees of ET, the piano scale, are
by definition related by factors of
21/12, and 21/12
is an irrational number, we cannot
escape the conclusion that no two
ET tones (other than the unison and
octaves) can form a consonant interval.
The intervals in an octave are 1 (i.e.
20), 21/12,
21/6, 21/4,
21/3, 25/12,
21/2, 27/12,
22/3, 23/4,
25/6, 211/12,
2 (i.e. 21), all of which,
except 1 and 2, are irrational.
I sometimes wonder
just how such a temperament ever gained
its monopoly in our music. Up until
around the time of Handel, all music
was based on Just Intonation (JI),
which we shall consider in a moment.
It seemed that there was some difficulty
in developing keyboards (lately gaining
in popularity) which could cope effectively
with JI. So, with a zeal more characteristic
of late twentieth century business
corporations, Keyboards Inc. set
about "effective management"
of its "customer perceptions".
Handel, bless his
cotton socks, resisted manfully, maintaining
for some time a keyboard with additional
keys which did support JI intervals.
Ironically, the keyboard lobbyís victory
actually made life harder for players
of other instruments. In particular,
brass players (trombonists apart!)
now had to "force" their intonation
to fit, and it seems nobody has ever
made any serious effort to remedy
this: to this day, brass pitching
is perforce "approximate". The key
point, though, and the one that impressed
Harry Partch, is that the crucial
purity of musical intonation
was sacrificed on the altar of business
convenience - a close parallel to
his own experiences. Exactly why this
is crucial is something that we will
tackle shortly.
. . . and Ring
In the Old
All musical intervals
are based on ratios: two tones
are related by the ratio of their
frequencies. There are natural laws
relating to vibrating strings. A string,
stretched between two fixed points,
will resonate in only certain modes.
These correspond to divisions of its
length into integral numbers of half-wavelengths.
The same is true, though less visibly,
of the vibrating columns of air in
wind instruments, and in a more complex
way in two dimensional bodies like
drumskins or three-dimensional ones
such as our old friends, the "coconut
shells"!
The "harmonic series"
of a vibrating string is often used,
all too briefly, as a starting point
for traditional teaching of music
theory, just before turning to the
piano and demonstrating its application.
Teachers seem to be either ignorant
of the fact that the ET scale of the
piano, based as it is on paradoxical-sounding
irrational ratios, does not actually
correspond at all, or at best dismiss
the differences as "insignificant"
- regardless of the fact that similar
"insignificant" differences in the
tuning of instruments in an ensemble
would sound ghastly.
The "natural" JI
intervals are based on ratios of small,
whole numbers, corresponding exactly
to the harmonics of that vibrating
string. Unison is 1/1, an "octave"
is 2/1, and other common ones are
3/2 and 5/4, so that for example a
3/2 implies
higher tone = 3 x (lower
tone)/2
These conform to
Galileo's definition of "agreeable
consonances": for a 5/4 the vibrations
are exactly in step once every 5 cycles
of the higher tone, corresponding
exactly to once every 4 cycles of
the lower. Any such ratio can be "reduced"
into the range 1 to 2 by a process
of doubling or halving either of the
numbers. For example 7/3, which is
bigger than 2, becomes 7/6, which
is between 1 and 2, by doubling the
lower number. This is nothing more
than our common practise of "octave
transposition".
It also highlights
the importance of the 2/1 interval.
Long history and much experimentation
have shown that the human ear recognises
some tones as distinct, and
others as distinctly not. The
ear will recognise the difference
in pitch of the two tones of a 2/1
interval, but will not afford them
a different identity, broadly
because every time the lower tone's
vibration is at a peak or trough,
so is the higher tone's. However,
the reason for this is not too important
here: it is in any case a physiological
axiom, true of any scale - JI, ET,
Mean Tone, or whatever. The intervals
5/2 and 5/4 have the same identity,
that is, both represent the same degree
of a JI scale, just as A and A' both
have the identity A in ET. In JI,
reducing a ratio to between 1 and
2 is equivalent to (say) referring
to "G" without saying which octave
it's in.
The preference shown
by the human ear - and that of a dog,
a cat, or a bat, for all we can tell
- for JI intervals over ET ones is
also a physiological axiom, notwithstanding
both biophysical considerations and
that this is exactly what Galileo
was driving at. Partch used to stage
experiments during lectures, playing
corresponding chords in both systems
to the "innocent ears" of his audience,
who would then be invited to vote
for which they preferred. Always,
and overwhelmingly, the JI chords
were preferred to the ET equivalents.
The reason for this
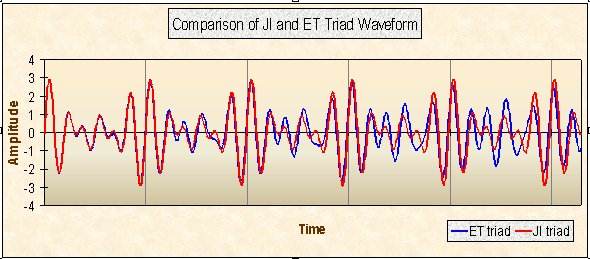
is illustrated in Fig. 1, a
comparison of the waveforms for an
ET major triad (like C-E-G) and the
equivalent JI triad (1/1-4/3-3/2).
The strongest peaks correspond to
the frequency of the tonic. You can
clearly see that the JI curve replicates
exactly in each cycle between
pairs of these peaks - in accord with
Galileo's dictum. The ET curve sets
out in step with the JI, but soon
diverges and, as mentioned earlier,
is never repeated exactly,
but varies progressively from cycle
to cycle, i.e. it is not consonant!
Evidence abounds
for the ear's inherent preference
for JI. Ensembles comprising only
instruments of continuously variable
pitch (such as violin family, voices,
trombones) in performance invariably
revert to JI, offering one tempting
reason why an a cappella choir,
for example, sounds so extraordinarily
beautiful. Then again, have you ever
wondered why the ear should enjoy
a smidgen of judicious vibrato, if
not to blur the dissonance inherent
in the ET scale? In a justly-intoned
performance, vibrato would actually
be detrimental to the sound, unless,
that is, it was being used to mask
poor intonation! More mundanely, I
have heard string players grumble
about how they have to play their
notes "a bit wrong" to fit in with
a piano, yet very rarely seem inclined
to wonder why!
Musical Scales
A scale is a sequence
of degrees, identities connecting
1/1 to 2/1. But what degrees, and
related by what intervals, actually
constitute a scale? Without any rules
to define the relationships, literally
"anything goes" - and possibly, right
now, a "glimpse of stocking" might
seem a little short of "something
shocking"? Why, for example, is our
ET fixed at only 12 identities? There
are 12 simply because the interval
is 21/12. There is no reason
why there should not be 24, with a
fixed interval between successive
identities of 21/24. Of
course, one or two composers in the
Twentieth Century have dabbled with
this "quarter-tone" scale. But why
not 19, or 3759, or even 42 (which
might appeal to aficionados of The
Hitch-hikerís Guide to the Galaxy).
Observing that the intervals are called
"semitones" leads nowhere either:
a "whole tone" is an equally arbitrary
21/6! The only reason for
12 would seem to be that this most
closely approximated the JI scale
current at the time that the ET scale
was invented.
JI intervals are
ratios of "small, whole numbers".
The question is: which numbers?
Mathematically, there is a sequence
of special numbers: 1, 2, 3, 5, 7,
11, 13, ... These are the prime
numbers, numbers which are exactly
divisible only by themselves or 1.
Prime numbers are crucial in JI largely
because of this property of irreducibility.
They prescribe sets of whole-number
ratios. The "ratios of N",
where N is a prime number, define
potential JI scales. Take 3, for example.
The ratios of 3 are
1/1 (unity), 4/3,
3/2, 2/1
These are all the
ratios which are possible, using prime
numbers no greater than 3. They have
been transposed into the range 1 to
2: the ratio 4/3 is musically identical
to 2/3 (as 4 is a doubling of 2).
Seeing as ratios of 1 (1/1 alone,
poor Johnny One-Note) and 2 (1/1,
2/1 only, Johnny and his boring sister
Joan) provided only a single identity,
and consequently virtually zero musical
potential, it comes as no surprise
that the ratios of 3 formed the basis
of the most primitive scales. After
the 1/1 (unison or unity) and 2/1
("octave"), 4/3 and 3/2
are the most powerfully consonant
intervals, both alive - though not
entirely well - in ET's "perfect
fourth" and "perfect fifth".
Without recourse to matters celestial
or divine, the meaning of "perfect"
is suddenly crystal clear!
The ratios of 5 are
1/1, 6/5, 5/4,
4/3, 3/2, 8/5, 5/3,
2/1
again, transposed
into the range 1 to 2. Notice that
the set of ratios of 3 (shown in
bold) necessarily appears as a
subset. As time progressed, more of
these intervals became recognised
as "consonant", in the sense
that they became "acceptable"
in musical terms. The sequence is
symmetrical, the intervals between
the degrees widening from the centre
outwards. Such gaps were closed, to
provide a more melodious spacing,
by the entirely legitimate use of
multiple number ratios, that
is, ratios formed by combining simple
ratios of 5, e.g. 16/15, 9/8. These
are nothing more than "compound
intervals": a new interval results
from the adding of two intervals,
and to add two intervals you just
multiply their ratios. Thus 4/3 x
8/5 = 32/15, which is identical with
16/15, and 3/2 x 3/2 = 9/4, identical
with 9/8. The ratios of 5, with associated
compound intervals, form the basis
of the JI scale which was "converted"
to produce 12-tone ET.
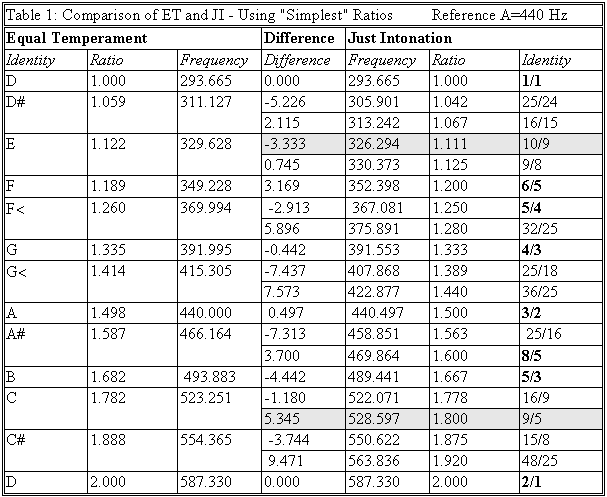
Table 1 shows how
the "conversion" might have
been made (I say "might",
because I have derived this representation
myself, from first principles). The
ratios of 5 identities are shown in
bold, and all the multiple
number ratios are also shown. Two
(10/9 and 9/5) are shaded because
these are not represented in ET (you
win some, you lose some - these are
where the pairs of JI alternatives
are relatively close - another example
of operational convenience?). The
places where pairs of JI degrees were
reduced onto a single, approximate
ET degree can be seen clearly, as
can the familiar resulting pattern
of "white" and "black"
notes.
Note how each "black"
note has two possible corresponding
JI identities, one a bit lower and
the other a bit higher in frequency:
Handel's "JI keyboard" would
have retained these as distinct keys.
That the scale starts on D is due
(probably, though I am not going to
go into that here, as it isn't really
relevant) to the shift in concert
pitch - the JI scale would originally
have been transposed onto the key
of C. Some of the approximations,
as shown by the differences, are disturbingly
high.
In JI it is obviously
possible to use ratios of 7, 11 and
so on, and derive musical scales with
ever more identities to the "octave",
limited in practical terms only
by the ear's ability to distinguish
them. Of course, the higher the
numbers employed, the greater become
the degrees of comparative dissonance,
with consequent widening of the scale's
expressive potential.
There was at one
time a controversy over the "legality"
of the chord of the dominant seventh,
which related to an implied extension
beyond the 5 limit enshrined in ET.
Significantly, the introduction of
ET effectively closed the door on
the development of the expressive
potential of musical scales. Over
several hundred years, we had moved
from 3-limit ratios to full use of
5-limit ratios. There is no reason
to suppose that this development would
have stopped there, had not the imposition
of ET "crystallised" the
5-limit.
Part
2 Part
3

